Pratical MPC
It is hard to construct threshold signing for ECDSA
In ECDSA:
\( s= k^{-1}(h+d_Ar) \bmod q \).
If we shares k1,k2, such that:
\(k_1 + k_2=k \bmod q \)
it is very difficult to compute \( k_1',k_2' \), such that
\( k_1'+k_2'=k^{-1} \bmod q \)
Two-party protocol in [4]
[4]use multiplicative sharing of x and k. That is the parties hold \(x_1,x_2\) such that \( x_1\cdot x_2=x \bmod q \),and in each signing operation they generate \(k_1,k_2\) such that \( k_1 \cdot k_2=k \bmod q \). For example:
\(P_1: c_1=Enc(k_1^{-1} \cdot H(m)), c2=Enc(k_1^{-1} \cdot x_1 \cdot r )\)
Then , using scalar multiplication(denoted \(\odot\)) and homomorphic addition(denoted \(\oplus\))
\( P_2: (k_2^{-1} \odot c_1)\oplus [(k_2^{-1} \cdot x_2)\odot c_2] \)
which will be an encryption of
\( k_2^{-1} \cdot (k_1^{-1}\cdot H(m)) + k_2^{-1}\cdot x_2\cdot(k_1^{-1} \cdot x_1 \cdot r)= k^{-1} \cdot (H(m)+ r\cdot x) \)
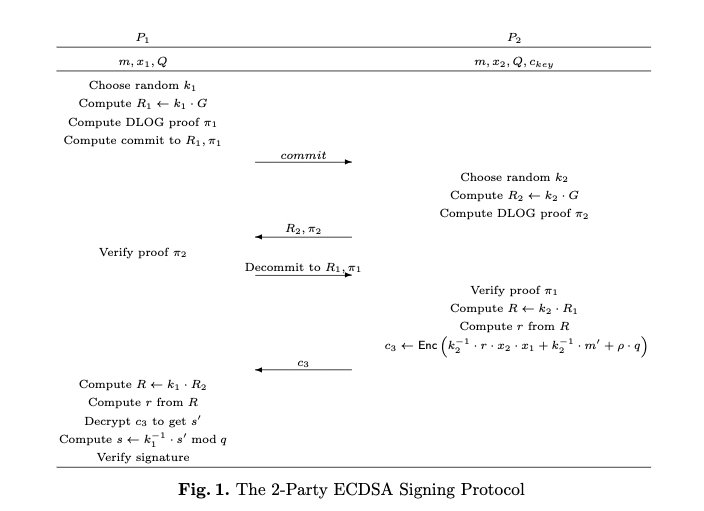
Two-party protocol in [2]
- P2 hold \( Enc(x_1), x2, \)
- P1 and P2 generate \( R=k_1 \cdot k_2 \cdot G \) by Diffle-Hellman key exchange with zkp
- P2 compute the encryption version of: \( k_2^{-1}\cdot H(m)+k_2^{-1}\cdot r \cdot x_1 \cdot x_2 \)
- P1 decrypt and multiplies the result by \( k_1^{-1} \)
Rotate share
In the implemention of unbound_security, when refresh share, they actually refresh the paillier's ek(encode key pair), dk(decode key pair).
Because Party_2 hold the encrypted x_1, if the paillier's dk is leaked, Party_2 can construct the private key.
In the above eqution, it seems that we can refresh \( x_1, x_2 \) at the same time, because \( x_1 \times r \times x_2 \times r^{-1} = x_1 \times x_2 \).
todo
- carrying out private-key operations via a secure protoco that reveals nothing but the output.
- revoke a party`s share.
- Is it possible to construct a full-threshold protocol for multiparty ECDSA, with practicaldistributed key generation and signing?
- It is possible for P1 to singlehandedly cmpute r from \( R=(r_x,r_y) \)
- Generate generic secret,then use to derivate bip. Is this safe?
References
- https://docs.particle.network/security
- Fast Secure Multiparty ECDSA with Practical Distributed Key Generation and Applications to Cryptocurrency Custody
- Fast Secure Two-Party ECDSA Signing
- Threshold-optimal DSA/ECDSA signatures and an application to Bitcoin wallet security
- unbound security github
- unbound security white paper
- Commitment schema wiki
- The Simplest Protocaol for Oblivious Transfer