快速傅立叶变换(Fast Fourier Transform)
复数的几何表示法
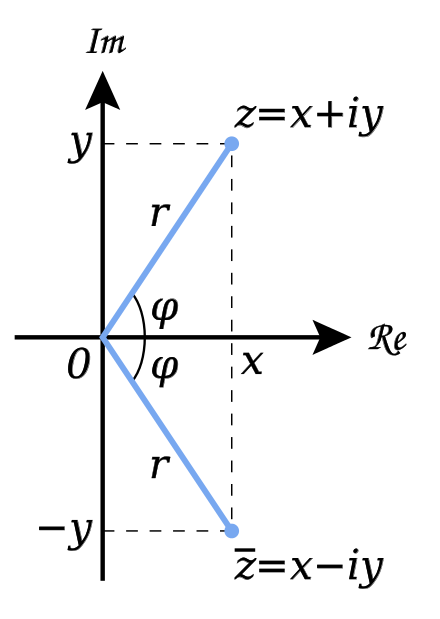
复数通过复平面来表示,复平面由水平的实轴和垂直的虚轴构成。一个复数的实部用沿x轴的位移表示,虚部用沿y轴的位移表示。上图中的复数$z=x+iy $ 也可以写做 $z=r(\cos{\varphi}+ i\sin{\varphi}) $, 如果r=1(单位圆),则 $z=\cos{\varphi} + i\sin{\varphi} $。
欧拉公式 (Euler's formula)
欧拉公式的作用是复分析领域的函数,它将三角函数与复指数函数关联起来。对任意的实数 x,都存在 $$e^{ix}=\cos{x} + i\sin{x} $$ 其中e是自然对数的底数,i是虚数单位。
单位根
将一个单位圆进行n等分,在单位圆上可以得到n个复数,设幅角为正且最小的复数为$\omega_n $, 称为 n次单位根,即 $$\omega_n=\cos{\frac{2\pi}{n}} + \sin{\frac{2\pi}{n}} $$ 根据欧拉公式有 $$\omega_n^k= \cos{\frac{2k\pi}{n}} + i\sin{\frac{2k\pi}{n}} $$ 特别地 $$\omega_n^0=\omega_n^n=1 $$
快速傅立叶变换
对于多项式$f(x)=\sum_{i=0}^n a_i x^i, g(x)=\sum_{i=0}^n b_i x^i $, 定义其乘积 fg 为
$$ (fg)(x)=(\sum_{i=0}^n a_i x^i)(\sum_{i=0}^n b_i x^i) $$
显然我们可以以$O(n^2) $的复杂度计算这个乘积的每一项的系数。
但 FFT 可以以 $O(n\log n) $的复杂度来计算这个乘积。
对多项式$f(x)=\sum_{i=0}^{n-1} a_ix^i $ ,不失一般性地设 $n=2^s, s\in N $,按照 $a_i$ 下标的奇偶性将 $f(x)$ 中的项分为两部分,即 $$\begin{align} f(x) &=(a_0+a_2x^2+a_4x^4+\cdots+a_{n-2}x^{n-2}) \ &+(a_1x+a_3x^3+a_5x^5+\cdots+a_{n-1}x^{n-1}) \ \end{align} $$ 令 $$ f_1(x)=a_0+a_2x^1+a_4x^2+\cdots+a_{n-2}x^{\frac{n}{2}-1} \ f_2(x)=a_1+a_3x+a_5x^2+\cdots+a_{n-1}x^{\frac{n}{2}-1} $$ 则 $$f(x)=f_1(x^2)+xf_2(x^2) $$
代入$x=\omega_n^k, (k<\frac{n}{2}) $可得 $$\begin{align} f(\omega_n^k) &=f_1(\omega_n^{2k}) + \omega_n^k f_2(\omega_n^{2k}) \ &= f_1(\omega_{\frac{n}{2}}^k) + \omega_n^k f_2(\omega_{\frac{n}{2}}^k) \end{align} \qquad(1) $$
代入$x=\omega_n^{k+\frac{n}{2}} $可得 $$\begin{align} f(\omega_n^{k+\frac{n}{2}}) &= f_1(\omega_n^{2k+n}) + \omega_n^{k+\frac{n}{2}} f_2(\omega_n^{2k+n}) \ &= f_1(\omega_{\frac{n}{2}}^k) - \omega_n^k f_2(\omega_{\frac{n}{2}}^k) \end{align} \qquad(2) $$
观察(1),(2)两式的结构,我们只需要求出$f_1(\omega_{\frac{n}{2}}^k), f_2(\omega_{\frac{n}{2}}^k) $即可在$O(1) $复杂度求出(1),(2)两式的值,进而再经过类似的步骤,我们可以将问题转化为求 $f_1(\omega_{\frac{n}{4}}^k),f_2(\omega_{\frac{n}{4}}^k) \cdots $,最终问题被转化为求 $$f_1(\omega_1^k)=f_2(\omega_1^k)=1 $$ 故而以$O(\log n) $的时间复杂度可以求出 $f(\omega_n^k), f(\omega_n^{k+\frac{n}{2}}) $,进而可以以$O(n\log n) $的时间复杂度求出所有的$f(\omega_n^k) $, 即我们以$O(n\log n) $的时间复杂度将f的系数表示法转化成了点值表示法。